Piece of Wire
Parabola
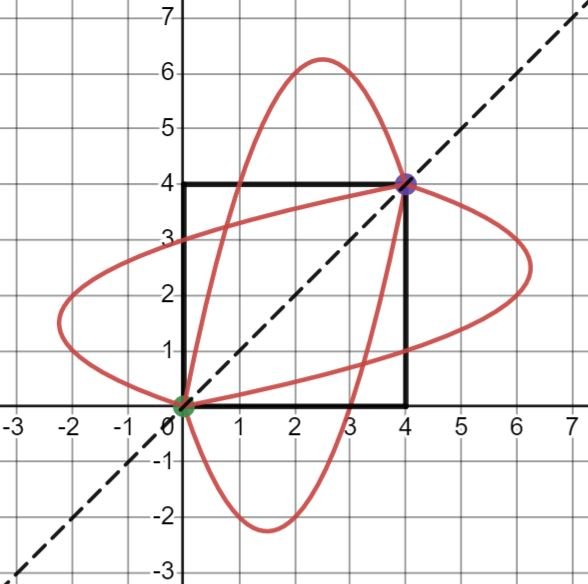
Suppose that the curve is a stiff piece of wire that you can lift up and reposition in different ways so that its end points are at (0,0) and (4, 4). How many different curves can you get? We ask the students to find these and plot them on Desmos.
This turns out to be a great exercise. Some of the students will be able to do this in their head. They will fairly easily see the solutions and sketch them on the diagram.
The final diagram showing all four curves has some lovely symmetry. To plot these on Desmos, they need to find equations for these four curves, and we expect that the graphical symmetries will help them to do that.
Hyperbola
You job is to cut out a finite piece of that graph and transform it so that it matches the graph in the second diagram. That is, it runs between the points (0, 0) and (4, 4) and has a concave-down shape. In transforming it you are allowed the following operations—you can translate it and you can reflect it in either axis.
Your job is to find the cut points in the graph and then find a formula for the function .